Calculadora de tasas de interés. La tasa de interés es la tarifa cobrada por el uso del dinero y se expresa como un porcentaje que se aplica al capital en diferentes unidades de tiempo (día, mes, trimestre, semestre, año, etc).
Quién no ha escuchado hablar de tasas de interés en el mundo financiero y ha pensado que todo es un enredo: que la tasa efectiva anual, la tasa mes vencido, la tasa semestre anticipado, la tasa nominal trimestre vencido; que si deposita su plata en tal inversión va a recibir tal tasa de rentabilidad. ¿Donde encuentro una calculadora de tasas de interés? Todas estas son expresiones en porcentaje que denotan el costo del dinero en un periodo de tiempo, en caso de un préstamo; o la rentabilidad del dinero en caso de una inversión. En este artículo te explicaremos qué son las tasas y podrás encontrar totalmente gratos la calculadora de tasas de interés Lyntik.
Por un lado están las tasas nominales:
Denotan una tasa con un periodo de capitalización o generación de interés mensual, bimestral, trimestral, semestral o anual. Con esta tasa se denota solo la causación de un interés en un periodo de tiempo y es este el que se agregará al capital de manera compuesta, que después se verá reflejado en el interés efectivo.
La tasa nominal suele estar referenciada en un periodo de un año, se muestra en porcentaje, se apellida con un periodo de capitalización y se cuña con un momento en el que se cobra: anticipada o vencida.
Ejemplo:
2% MV = dos por ciento mes vencido.
1% SA = uno por ciento semestre anticipado.
Por otro lado están las tasas efectivas:
Expresan el costo o la rentabilidad como una tasa de interés compuesta teniendo en cuenta la acumulación de intereses. en este artículo no se profundizará en lo que es la tasa compuesta, solo bastará con decir que suma intereses al capital para la nueva causación. En este sentido, es la tasa realmente cobrada para un periodo de tiempo. En este caso vamos a suponer, para efectos de mejor entendimiento y de acercamiento a la vida comercial, que las tasas efectivas denotan automáticamente su periodo de capitalización.
Todas las tasas, de cualquier tipo y en cualquier periodo, se pueden traducir en el tiempo para encontrar su equivalencia. Para esto, partamos de los siguientes supuestos:
- Periodicidades en un año:
Meses al año: 12
Bimestres al año: 6
Trimestres al año: 4
Semestres al año: 2 - Con tasas nominales se puede cambiar la periodicidad solo con dividir o multiplicar: pasar de anual a mensual, de mensual a trimestral, de trimestral a bimestral, etc. En este caso lo único que se debe hacer es multiplicar o dividir la tasa por la periodicidad. Ejemplo: encontrar la tasa semestral de una tasa de 2% MV.
2% x 12 (meses al año) = 24% AV y esta tasa la trasladaremos a la tasa semestral: 24% / 2 (semestres al año) = 12% SV.
O directamente: 2% x 6 (un semestre equivale a seis meses) = 12% SV. - Con las tasas efectivas, como se suponen periódicas, se pueden aplicar las siguientes formulas directamente para cambiar su periodicidad:
- Para pasar a una periodicidad mayor:
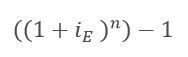
iE= Interés Efectivo
n = Número de periodos
Ejemplo: ¿Cuál es la tasa efectiva anual correspondiente a una tasa del 2% mensual?
iEM (Interés Efectivo Mensual) = 2%
n = 12 meses
→ iEA (Interés Efectivo Anual) = ((1 + 0.02) ^12) – 1 = 26.82% EA
- Para pasar a una periodicidad menor:
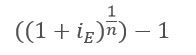
iE= Interés Efectivo
n = Número de periodos
Ejemplo: ¿Cuál es la tasa efectiva trimestral correspondiente a una tasa del 24% EA?
iEA (Interés Efectivo Anual)= 24%
n = 4 trimestres
→ iET (Interés Efectivo Trimestral)= ((1 + 0.24)^1/4) – 1 = 5.53 % ET.
4. Después de encontrar equivalencias en el tiempo se puede convertir la tasa nominal en la tasa efectiva o la efectiva en nominal.
- Pasar de Efectivo (iE) a Nominal (iN):
iE= Interés Efectivo
n = Número de periodos
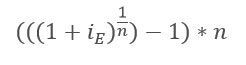
Ejemplo: ¿Cuál es la tasa nominal anual correspondiente a una tasa del 24% efectivo anual?
iEA (Interés Efectivo Anual)= 24%
n = 12 meses
→ iNA (Interés Nominal Anual)= ((1 + 0.24)^1/12) – 1)*12 = 21.71% NA
- Pasar de Nominal a Efectiva:
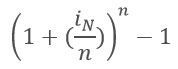
N = Interés Nominal
n = Número de periodos
Ejemplo: ¿Cuál es la tasa efectiva anual correspondiente a una tasa del 24% nominal anual?
iNA = 24%
n = 12 meses
→iEA = (((1 + (0.24/12))^ 12) – 1 = 26.82% EA
Da clic en el botón ‘Ir a la calculadora‘ y comienza a usar la calculadora de tasas de interés Lyntik totalmente gratis.
